Generators of Profiles#
[1]:
import svvamp
Impartial Culture#
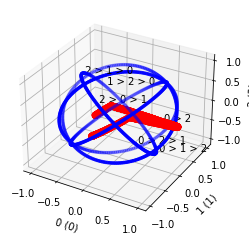
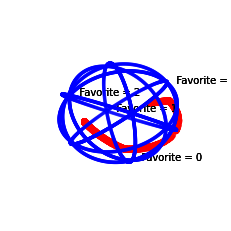
The Spheroid model is an extension of the Impartial Culture to utilities:
[2]:
profile = svvamp.GeneratorProfileSpheroid(n_v=100, n_c=5)()
profile.plot3()
profile.plot4()
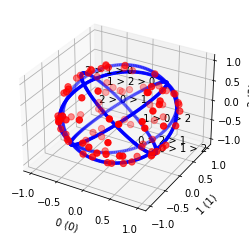

The Cubic Uniform model is another one:
[3]:
profile = svvamp.GeneratorProfileCubicUniform(n_v=5000, n_c=3)()
profile.plot3(normalize=False)
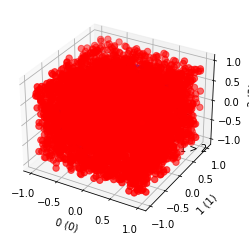
[4]:
profile = svvamp.GeneratorProfileCubicUniform(n_v=5000, n_c=4)()
profile.plot4(normalize=False)
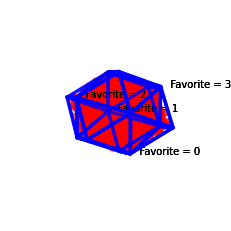
Neutral Culture with Weak Orders#
The Ladder model is also neutral (it treats all candidates equally) and voters are also independent, like in Impartial Culture, but weak orders are possible.
[5]:
profile = svvamp.GeneratorProfileLadder(n_v=1000, n_c=3, n_rungs=5)()
profile.plot3(normalize=False)
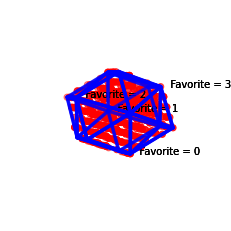
[6]:
profile = svvamp.GeneratorProfileLadder(n_v=1000, n_c=4, n_rungs=5)()
profile.plot4(normalize=False)
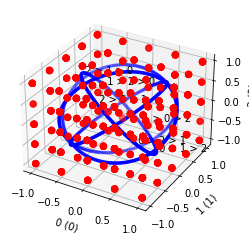
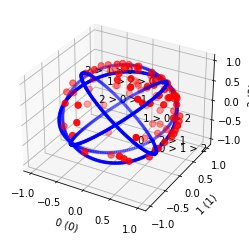
Polarized Cultures#
The Von-Mises Fisher model represents a polarized culture. There are two variants (hypersphere and hypercircle).
[7]:
profile = svvamp.GeneratorProfileVMFHypersphere(
n_v=100, n_c=5, vmf_concentration=20)()
profile.plot3(indexes=[0, 1, 2])
Political spectrum#
In these models, voters and candidates draw independent positions in a Euclidean space (the “political spectrum”). The utility of a voter v for a candidate c is a decreasing function of the distance between their positions. If the dimension of the political spectrum is 1, then the population is necessarily single-peaked (cf The theory of committees and elections, Duncan Black, 1958).
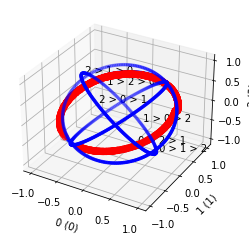
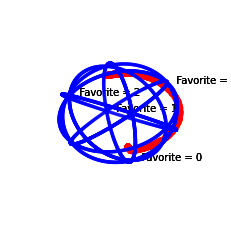
Gaussian Well model:
[8]:
profile = svvamp.GeneratorProfileGaussianWell(
n_v=1000, n_c=4, sigma=[1], shift=[0])()
profile.plot3()
profile.plot4()
Euclidean Box model:
[9]:
profile = svvamp.GeneratorProfileEuclideanBox(
n_v=1000, n_c=4, box_dimensions=[1])()
profile.plot3()
profile.plot4()