Profile#

[1]:

import svvamp

Define a random generator of profiles using the Spheroid model (which extends Impartial Culture to utilities), with 9 voters and 5 candidates:

[2]:

random_profile = svvamp.GeneratorProfileSpheroid(n_v=9, n_c=5)
random_profile

[2]:

<svvamp.preferences.generator_profile_spheroid.GeneratorProfileSpheroid at 0x21b46c98770>

Use the generator to create a random profile:

[3]:

profile = random_profile()

If you wish, you can give a label to each candidate:

[4]:

profile.labels_candidates = ['Alice', 'Bob', 'Catherine', 'Dave', 'Ellen']

Basic information about the profile:

[5]:

profile.n_v

[5]:

9

[6]:

profile.n_c

[6]:

5

[7]:

profile.labels_candidates

[7]:

['Alice', 'Bob', 'Catherine', 'Dave', 'Ellen']

Voters’ rankings of preference:

[8]:

profile.preferences_rk

[8]:

array([[2, 3, 1, 0, 4],
       [4, 2, 0, 3, 1],
       [4, 2, 0, 3, 1],
       [1, 2, 0, 4, 3],
       [4, 3, 0, 2, 1],
       [3, 1, 2, 4, 0],
       [1, 2, 3, 4, 0],
       [3, 2, 1, 4, 0],
       [4, 2, 0, 1, 3]])

Voters’ utilities for the candidates:

[9]:

profile.preferences_ut

[9]:

array([[-0.44458068,  0.14553558,  0.68052773,  0.16357809, -0.5397144 ],
       [ 0.0268188 , -0.67982384,  0.25992916, -0.19772748,  0.65609525],
       [-0.40017529, -0.78147922, -0.2535415 , -0.40465215,  0.03351569],
       [ 0.14343979,  0.50952062,  0.36903622, -0.76264855,  0.04464546],
       [-0.23395736, -0.71376382, -0.63007483, -0.19696857,  0.0037754 ],
       [-0.23303553,  0.46519408,  0.45194157,  0.70715693,  0.15800885],
       [-0.77027357,  0.45199658,  0.40743494,  0.17577499,  0.0740111 ],
       [-0.65635213,  0.20304854,  0.45371884,  0.54194463,  0.1685479 ],
       [ 0.0364911 , -0.59018254,  0.19841761, -0.74973679,  0.22108407]])

Plot the restriction of the population to 3 candidates, for example [0, 2, 3] (Alice, Catherine and Dave), in the utility space:

[10]:

profile.plot3(indexes=[0, 2, 3])
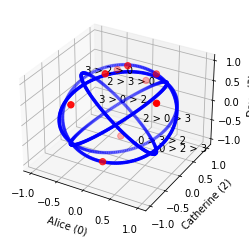
../_images/tutorials_tutorial_profile_17_0.png

Plot the restriction of the population to 4 candidates, for example [0, 1, 2, 4] (Alice, Bob, Catherine and Ellen), in the utility space:

[11]:

profile.plot4(indexes=[0, 1, 2, 4])
../_images/tutorials_tutorial_profile_19_0.png

Plurality score, Borda score and total utility of each candidate:

[12]:

profile.plurality_scores_ut

[12]:

array([0, 2, 1, 2, 4])

[13]:

profile.borda_score_c_ut

[13]:

array([11., 16., 25., 18., 20.])

[14]:

profile.total_utility_c

[14]:

array([-2.53162488, -0.98995401,  1.93738974, -0.72327889,  0.8199693 ])

Matrix of duels (weighted majority graph) and matrix of victories (unweighted majority graph):

[15]:

profile.matrix_duels_ut

[15]:

array([[0, 4, 1, 4, 2],
       [5, 0, 3, 3, 5],
       [8, 6, 0, 6, 5],
       [5, 6, 3, 0, 4],
       [7, 4, 4, 5, 0]])

[16]:

profile.matrix_victories_ut_abs

[16]:

array([[0., 0., 0., 0., 0.],
       [1., 0., 0., 0., 1.],
       [1., 1., 0., 1., 1.],
       [1., 1., 0., 0., 0.],
       [1., 0., 0., 1., 0.]])

Condorcet winner:

[17]:

profile.condorcet_winner_ut_abs

[17]:

2

By convention, if there is no Condorcet winner, then SVVAMP returns nan (not a number).